DDS (Digital Direct  Synthesis)  

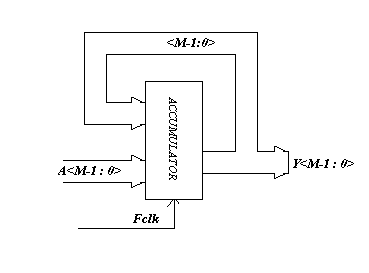
Introduzione

 In questo documento sono esposte tutti i concetti teorici che stanno alla base della tecnica DDS. Prima di passare in rassegna la tecnica DDS saranno dati alcuni cenni su i singoli blocchi che costituiscono il sistema DDS

 L’accumulatore

 L’accumulatore è un circuito digitale, sincrono, che esegue ad ogni ciclo di clock la somma tra due quantità di cui una è un ingresso esterno e l’altra è la sua uscita. Quindi esso “accumula” nella sua uscita i vari risultati delle somme effettuate nei cicli. In pratica, l’accumulatore è un sommatore la cui uscita è connessa ad uno dei suoi ingressi. In figura 1 è riportato uno schema di massima di un accumulatore:

Fig. 1: schema di un accumulatore a M bit.

 In genere, come specifica dell’accumulatore, sì da il numero di bit della sua uscita. Per un accumulatore di M bit s’intende un accumulatore la cui uscita è costituita da M bit. In genere si afferma che l’accumulatore va in overflow: ciò significa che se il risultato della somma tra la sua uscita e il dato in ingresso e pari ad un numero per la cui rappresentazione sono necessari un numero di bit maggiori di M. In tal caso si afferma che l’accumulatore “wraps around” ovvero la sua uscita assumerà il valore che rappresentano i primi 16 bit della somma che ha provocato l’overflow.
Un esempio per capire l’overflow:
Supponiamo di avere un accumulatore di 8 bit. Il valore massimo in uscita sarà 255d (FF h). Poniamo l’ingresso a 100d (64h) e indichiamo con Y l’uscita, avendo posto inizialmente Y(0) =0 ovvero di aver resettato l’uscita prima di cominciare. 

passo 1:

 Y(1)= Y(0)+ 100 = 0 + 100 = 100  < 255

 passo 2:

 Y(2)= Y(1)+ 100 =100+100 = 200 < 255

 passo 3:

 Y(3)= Y(2)+ 100 =200+100 = 300 > 255  !!! overflow

 Siamo in condizione di overflow poiché il risultato richiede un numero di bit maggiore di 8 precisamente 9. L’uscita Y conterrà i primi 8 bit del risultato ovvero:

 300d = 1 0010 1100 b di cui i primi 8 bit sono 0010 1100 quindi Y(3)= 0010 1100 = 44

 In termini matematici significa che l’uscita dell’accumulatore è pari alla divisione modulo 2^N