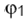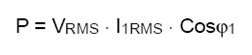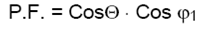Segnali sinusoidali non ideali

Se la corrente e’ un segnale periodico ma non sinusoidale ovvero distorto,  per calcolare il suo valore RMS dobbiamo ricorrere alla trasformata di Fourier che ci permette di ricavare tutte le sue componenti in frequenza.Il valore RMS della corrente è dato dalla segunete relazione:

 

Dove I₀ e’ la componente in continua (DC) della corrente Irms. Il termine I_1RMS e’ la componente detta fondamentale della corrente Irms in quanto alla frequenza della tensione che gennera la tensione I.  I termini  I_2RMS….I_nRMS rappresentano il valore RMS delle armoniche dovute alla distorsione del segnale o al fatto che non sia una sinusoide pura. 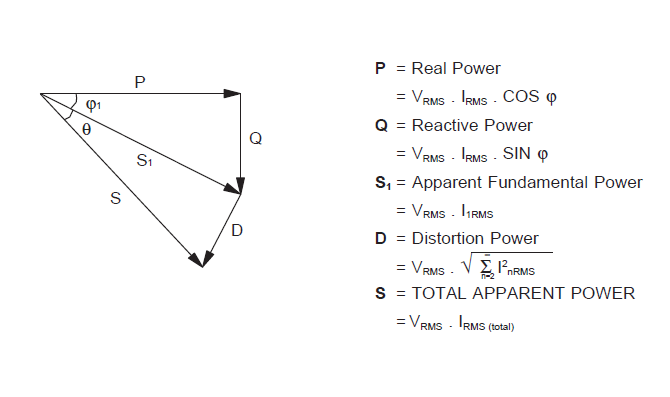Per un segnale sinusoidale puro, il valore della componente continua I₀  e le armoniche  di ordine maggiore o uguale a due sono nulle.
La componente fondamentale I_1RMS ha una componente in fase che indichiamo con I_{1RMS_P} ed una componente in quadratura che indichiamo con I_{1RMS_Q}. Cosi la formula della I_RMS totale può essere riscrita tenendo conto del fatto che il termine relativo alla fondamentale I_1RMS può essere espress come somma dei quadrati delle sue componenti I_{1RMS_P e} I_{1RMS_Q}:

La potenza attiva P e’ data dal prodotto del valore RMS della tensione con la componente RMS in fase della fondandamentale della corrente ovvero:

Se indichiamo con 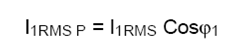 l’angolo di sfasamento tra la tensione di ingresso con la componente fondamentale, il valore RMS della componente in fase della corrente   I_1RMS. e’ dato dalla relazione:

E quindi la potenza reale:

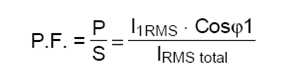
La potenza apparente S è data dal prodotto del valore RMS della tensione e il valore RMS della corrente, ovvero:

Il fattore di potenza, in base alla sua definizione  allora si puo esprimere come:

Introducendo il fattore K definito come:

 Dove e’ detto l’angolo di distorsione.

Il fattore K e’quindi collegato al contenuto armonico della corrente. Se il contenuto armonico della corrente e’ prossimo allo zero (caso sinusoide) allora K tende al valore unitario.  In conclusione la definizion del PF puo essere riscritta come:

 La rappresentazione vettoriale della formula della potenza apparente nel caso non sinusoidale in presenza di distorsione e’ quindi:

La potenza reattiva Q  e la potenza di distorsione D, producono delle correnti RMS maggiori aumentando le  perdite e riducendo l’efficienza della rete di alimentazione.