|
|
|||
|
Convertitore analogico - digitale SIGMA DELTA |
|||
|
|||
|
|
|||
|
I
convertitori analogico digitali Sigma Delta offrono un elevata
risoluzione, alta integrazione, basso costo. Tutte queste
caratteristiche rendono i Sigma Delta ottimali per tutte
quelle applicazioni come controllo di processi e misure. Spesso i
progettisti scelgono gli ADC di tipo SAR perché non conoscono bene le
caratteristiche dei convertitori Sigma Delta.
La parte analogica del convertitore Sigma Delta e' molto semplice in quanto si tratta di un convertitore analogico-digitale ad 1 bit. La parte digitale, che rende il SD molto costoso da produrre, e' molto più complessa. Questa parte esegue le funzioni di filtraggio e di decimazione. Per capire come questa funziona bisogna avere familiarità con i concetti di sovra-campionamento ( oversampling), noise shaping, filtraggio e decimazione. Nel resto del documento con SD si indicheranno i convertitori analogico- digitali Sigma Delta.
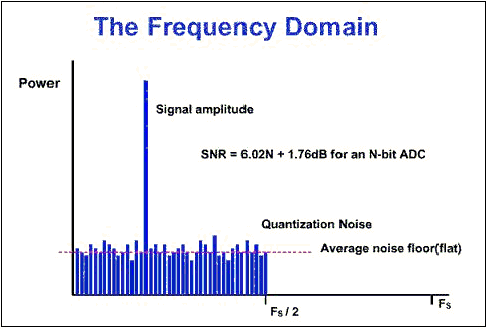
Sovra-campionamento (oversampling) Consideriamo un tradizionale ADC multi bit nel domino della frequenza avente un segnale sinusoidale in ingresso campionato alla frequenza Fs. In accordo con la teoria di Nyquist, la Fs deve essere almeno il doppio della banda del segnale da campionare. Osservando il risultato della analisi FFT del segnale di uscita digitale dell'ADC ( figura 1), si nota la presenza della riga corrispondente alla frequenza del segnale sinusoidale in ingresso e alla presenza di altri segnali sparsi in maniera random nell'intervallo che va dalla DC ( frequenza zero detta continua) alla frequenza Fs/2. L'insieme di questi segnali viene definito come rumore (noise). Questo tipo di rumore e' noto come rumore di quantizzazione ed possibile spiegarlo in tal modo: il segnale in ingresso all' ADC e' continuo e può assumere infinti valori. L'uscita del ADC e' digitale ed e' una funzione discreta che può assumere sono determinati valori definiti dalla risoluzione dell'ADC. Quindi la conversione da analogico ad digitale comporta la introduzione di distorsione nel segnale di uscita del ADC e la perdita di informazioni sul segnale con conseguente errore pari al massimo al valore associato al bit LSB =1/2^N ( N numero di bit dell'ADC).
Figura 1: FFT del segnale di uscita di un ADC a N bit con frequenza di campionamento Fs |
|
||
|
|
|||
|
|
|||
|
|
|||