|
Per rimuovere tali limitazioni, occorre dunque sostituire
la grandezza manipolabile Y con una grandezza non più digitale (ON-OFF)
ma analogica, capace di assumere un certo insieme di valori intermedi
alle due situazioni estreme. Si potrà quindi fornire al sistema una
potenza anche intermedia, come per esempio il 25% oppure il 70% e così
via; in questo modo si avrà un maggior grado di libertà nel controllare
la potenza fornita al sistema.
Anche le variabili di set point e di valore reale andranno trattate in
modo diverso: il comparatore non fornirà più alla sua uscita un valore
a soli due stati (ON-OFF) dipendente dal fatto che una delle grandezze
supera l'altra, ma un valore analogico contenente anche
l'informazione di quanto le due grandezze differiscono. La grandezza
analogica che si viene così ad introdurre verrà chiamata ERRORE e sarà
nel seguito indicata con X; più precisamente la variabile X
rappresenterà, istante per istante, la differenza tra le due grandezze
omogenee di set point S e di valore reale misurato R.
A questo punto viene naturale introdurre un blocco funzionale F nel
sistema di controllo capace di generare un opportuno valore della
grandezza manipolabile Y in funzione esclusivamente del valore
dell'errore X:
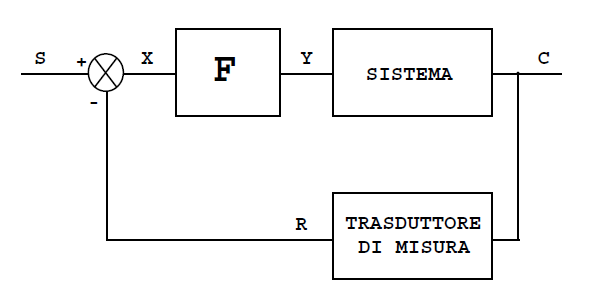
Figura 3: schema a blocchi di
un sistema di regolazione con controllore F
Il blocco funzionale F ha l'incarico di pilotare il
sistema mediante la sua uscita Y (grandezza manipolabile) avendo come
unica informazione il valore della variabile errore X.
La funzione F può avere diverse forme realizzative, corrispondenti a
specifiche rappresentazioni matematiche; la più semplice funzione
matematica che ci può venire in mente è quella lineare:

Un blocco funzionale del genere permette di fornire
potenza al sistema in modo proporzionale al valore corrente
dell'errore; questo significa che se il valore reale misurato si
discosta molto dal valore del set point desiderato, la potenza fornita
al sistema è prossima
ad uno dei due valori limite (0% oppure 100%) a seconda del segno della
variabile X. Più precisamente, nel dimensionare le grandezze in gioco
nel sistema fisico reale, si stabilisce una banda attorno al set point,
corrispondente alla variazione analogica della potenza fornita
al sistema; ciò equivale all'inserimento a valle del blocco F di un
blocco limitatore capace di bloccare il valore di Y ai valori limiti
permessi.
Un sistema di controllo in retroazione, utilizzante un blocco F di
questo tipo, viene chiamato "regolatore di tipo P" poiché il suo
comportamento è basato su un'azione di tipo proporzionale. Un
regolatore di tipo P lo si impiega in quei sistemi che permettono
un'elevata costante di guadagno d'anello senza incorrere in problemi di
stabilità.
La funzione F non deve necessariamente determinare il
valore corrente
della grandezza manipolabile Y basandosi esclusivamente sul valore allo
stesso istante della variabile errore X. Infatti notevoli miglioramenti
nelle prestazioni del controllo si ottengono utilizzando funzioni F che
tengano conto anche dei valori assunti dall'errore in precedenza.
Basti pensare che, conoscendo l'andamento nel tempo della variabile
errore, è possibile stabilire la velocità della variabile stessa
corrispondente ad un'informazione sulle capacità del sistema
controllato di rispondere alle sollecitazioni della grandezza
manipolabile Y. Ciò consente, in un certo senso, di prevedere la
reazione del sistema al controllo fornito mediante la grandezza Y e di
agire di conseguenza. In particolare alla funzione F si potrebbe
aggiungere un ulteriore termine costituito da una
funzione integrale della variabile errore:

Una regolazione con tale funzione F viene chiamata
"regolazione di tipo PI", in quanto la sua azione ha un effetto di tipo
integrativo oltre che proporzionale; questa funzione tiene memoria
della storia passata della variabile X, fornendo un'azione correttiva
capace di aggiungere o togliere la potenza in modo graduale al fine di
far avvicinare il valore reale R al set point S.
Infine ulteriori possibilità sono offerte da una funzione F
comprendente anche un termine derivativo:

L'azione derivativa, indicata generalmente con D,
permette di ottenere maggior prontezza di risposta nel controllo del
sistema, in quanto la correzione è tanto più elevata quanto rapida è la
variazione dell'errore.
La funzione alla quale siamo giunti prende il nome di funzione PID in
quanto comprende tutti e tre gli effetti correttivi. La funzione PID è
certamente la funzione correttrice più utilizzata nei sistemi di
controllo ad anello chiuso; essa infatti, per la sua generalità,
permette di adattarsi a gran parte dei sistemi da controllare. Variando
il peso dei tre termini è possibile configurare il sistema di controllo
alle più svariate esigenze ed è per questo che un regolatore di tipo
PID è anche chiamato regolatore STANDARD.
|



