|
Calcoli dei
parametri
I valori delle costanti considerate sono funzione del
sistema controllato e quindi non definibili a priori; queste costanti
costituiscono spesso un notevole ostacolo a chi si accinge a sviluppare
un controllo di tipo PID. Esistono infatti diversi metodi per il loro
calcolo, alcuni
strettamente empirici, altri più teorici basati su alcune formule che
richiedono tuttavia la determinazione di dati di partenza mediante
metodi sperimentali.
Un metodo frequentemente utilizzato è quello di misurare la risposta
del sistema ad anello aperto in seguito ad una sollecitazione a gradino
della variabile manipolabile. Tracciando un grafico dell'andamento
temporale della grandezza controllata dopo l'applicazione del gradino è
possibile determinare il tempo di risposta del sistema e da tale valore
è possibile dedurre i parametri ottimali del PID. Il metodo della
misurazione sperimentale della funzione di risposta al gradino risulta
abbastanza laboriosa e richiede una strumentazione adeguata.
Un metodo alternativo, dal quale discende l'algoritmo utilizzato per
l'autocalcolo dei parametri, è quello della determinazione della "banda
proporzionale di pendolazione". Abbiamo visto che, in assenza delle
azioni integrale e derivativa, l'equazione PID si riduce a:
Y= K X
dove la costante K è più propriamente detta "sensibilità
proporzionale". Si definisce "banda proporzionale" l'inversa della
sensibilità proporzionale e corrisponde alla variazione del valore
reale R necessaria per provocare una variazione unitaria della
variabile manipolabile Y.
Il metodo della banda proporzionale di pendolazione consiste nel porre
il sistema retroazionato in una condizione di stabilità limite,
corrispondente ad una situazione di oscillazione permanente: per far
ciò occorre momentaneamente escludere dall'anello le azioni integrale e
derivativa. In tale situazione di oscillazione permanente il valore
reale R oscilla in modo periodico attorno al valore del set point S,
con un'ampiezza ed un periodo dipendenti dalle caratteristiche fisiche
del sistema; misurando il valore della banda proporzionale 1/K0 del
sistema così ottenuto e del periodo T0 di oscillazione è possibile
calcolare il parametri ottimali della funzione PID applicando le
seguenti formule di Ziegler e Nichols:

Vediamo ora come applicare in pratica tale metodo e in
particolare come sviluppare un algoritmo capace di calcolare in modo
del tutto automatico tali parametri.
Per portare il sistema in una condizione di oscillazione permanente
nella quale l'azione integrale e derivativa non hanno effetto, occorre
considerare una forte prevalenza del fattore proporzionale: una simile
situazione la si ha per un sistema di controllo in retroazione del tipo
ON-OFF. Infatti se si considera un fattore di sensibilità K elevato,
delle piccole entità di errore X provocano degli elevati valori della
grandezza manipolabile Y, con conseguente saturazione ai due valori
limite estremi; questi due valori limite, nel caso in questione della
termoregolazione mediante potenza elettrica applicata ad una
resistenza, corrispondono alla situazione di potenza 100% e di potenza
0% e quindi riconducibile ad un ON-OFF.
Occorre dunque impostare una regolazione di tipo ON-OFF, attendere il
termine del primo ciclo di oscillazione attorno al set point per la
stabilizzazione dell'oscillazione ed infine calcolare il corrispondente
valore di banda proporzionale 1/K0 e di periodo T0 di oscillazione.
Applicando le precedenti formule si ricavano i parametri PID. Infine
sostituiamo la regolazione di tipo ON-OFF con la regolazione di tipo
PID utilizzante i parametri così ricavati.
La banda proporzionale, secondo la sua definizione,
corrisponde alla variazione del valore reale R necessaria per provocare
una variazione unitaria della variabile manipolabile Y. Nel caso della
regolazione ON-OFF abbiamo una variazione della grandezza manipolabile
Y tra i suoi due estremi (0% e 100%) e quindi pari al valore di fondo
scala (indicato con F.S.);
inoltre se misuriamo la variazione complessiva, indicata con A, del
valore reale R in un ciclo di pendolazione permanente (valore
picco-picco dell'oscillazione), possiamo calcolare la banda
proporzionale di pendolazione mediante la sua stessa definizione:
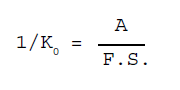
Per quanto riguarda la scelta del tempo T di
aggiornamento dell'equazione in genere si utilizza un valore pari a
1/20 del tempo T0 allo scopo di consentire una pronta reazione della
funzione PID alle variazioni delle condizioni fisiche del sistema
controllato. Si noti che dei
valori di T più bassi del necessario portano ad un elevato valore della
costante derivativa D con probabili saturazioni della variabile Y.
Valori di T più alti del necessario portano invece a bassi valori della
costante integrativa I e nel caso si eseguano calcoli solo tra interi
si può incorrere in troncamenti dei decimali tali da annullare tale
azione correttiva anche in presenza di una costante K premoltiplicata
per per una certa potenza del 10.
E' importante infine far seguire il blocco funzione PID da un blocco di
limitazione del valore Y tra un valore Ymin ed un valore Ymax
corrispondenti al range di variazione utile ed effettiva dell'uscita.
Infatti, a causa di improvvise e consistenti variazioni del setpoint, la
formula può produrre valori di Yn valori molto al di fuori dei limiti
suddetti e che non comportano ulteriori variazioni della variabile
controllata. La variabile Yn potrà, a causa della stessa natura della
formula PID, impiegare molto tempo per ritornare entro i limiti
consentiti con conseguente permanenza dell'uscita in uno stato di
saturazione.
Con l'introduzione dei suddetti limiti dell'uscita Y, il precedente
valore di fondo scala F.S. viene a corrispondere alla differenza (Ymax
- Ymin). Da ciò segue che il valore di K0 può essere ottenuto dal
rapporto tra questa differenza ed il valore picco-picco della variabile
d'errore X.
Di seguito è riportato un tipico andamento nel tempo del
valore reale R durante la fase preliminare di regolazione ON-OFF (nella
quale vengono calcolati i parametri PID) e successivamente durante la
fase di regolazione PID.

Figura 4: Determinazione dei parametri del sistema dalla
regolazione ON-OFF
|
|