Convertitore analogico - digitale SIGMA DELTA

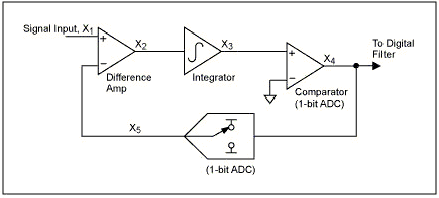
Noise Shaping

Per comprendere la tecnica del noise shaping facciamo riferimento alla schema blocchi di un modulatore sigma delta del primo ordine mostrato in figura 4

Figura 4: schema blocchi di un modulatore sigma delta del primo ordine

Un modulatore SD e' costituito da un amplificatore differenziale, da un integratore, da un comparatore e da un DAC ad 1 bit collegati ad anello chiuso. In particolare il DAC ad 1 bit altro non e' che un commutatore che da in uscita la tensione di riferimento positiva o negativa ( vdd o gnd nella maggior parte dei casi) a seconda se l'uscita del comparatore e' alta o bassa. La funzione del DAC, posto in retroazione, e' quella di porre il valore medio della tensione di uscita dell'integratore vicino al valore di riferimento del comparatore.
La densità di uni ( "1") presenti all'uscita e modulatore SD e' proporzionale al valore del segnale di ingresso. Incrementando la tensione di ingresso il comparatore genera un maggior numero di uni e viceversa al decrescere della tensione di ingresso genera un numero minore di uni. L'integratore in questo anello di controllo agisce come filtro passa basso per il segnale di ingresso ma come filtro passa alto per il rumore di quantizzazione. Cosi la maggior parte del rumore di quantizzazione e' posto ad alta frequenza come mostrato in figura 5.

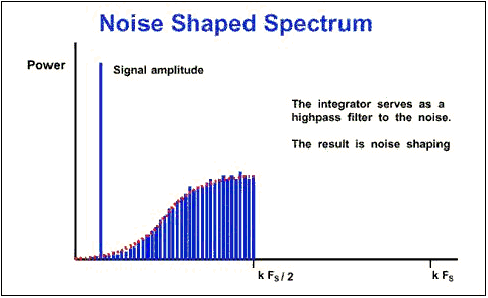
Figura 5: effetto dell'integratore sul segnale di uscita di un modulatore SD 

Questo dunque e' il noise shaping dovuto al sovra campionamento ovvero si ha una distribuzione del rumore in modo da mettere il rumore di quantizzazione ad alta frequenza allontanandolo dal segnale originale.

Applicando un filtro digitale al uscita del modulatore SD ,in cui e' presente  il noise shaping, si ha un maggiore riduzione del rumore come mostrato in figura 6.

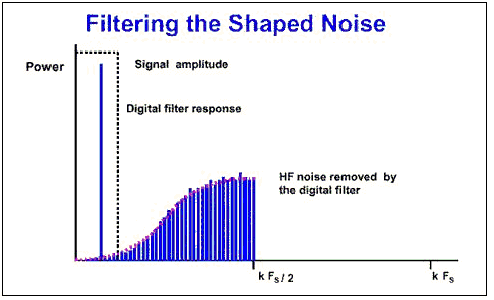
Figura 6: effetto del filtro digitale sul rumore modificato ( noise shaped) 

Questo tipo di modulatore del primo ordine fornisce un miglioramento di 9 dB sul SNR per ogni raddoppio della frequenza di campionamento. Per elevati ordini di quantizzazione, quindi maggiore rumore di quantizzazione, si può ottenere il noise shaping  utilizzando più di un stadio di integrazione e di somma nel modulatore SD.
In figura 7 e' mostrato il profilo del noise shaping nel caso di primo ordine ( linea rossa ) e nel caso si modulatore del secondo ordine ( linea blue). 

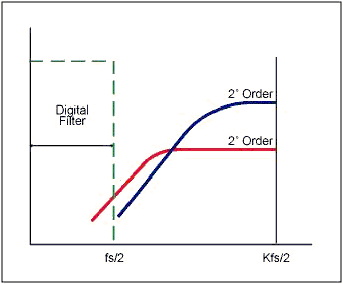
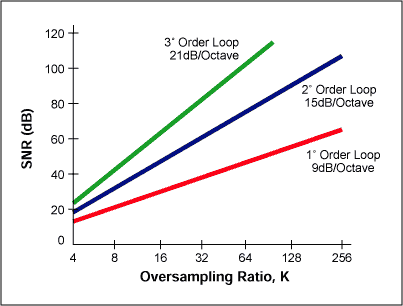
Figura 7 : profili di noise shaping per SD del primo (rosso) e secondo ordine           ( blue)

Come si vede il profilo del secondo ordine relega una quantità di rumore  di quantizzazione alle altre frequenze di quanto fa il profilo del primo ordine. In figura 8 e' riportato un diagramma che mette in relazione l'ordine del modulatore SD con  il fattore di oversampling per ottenere un dato SNR

Figura 8: relazione tra l'ordine del SD e il fattore di oversampling per  un dato SNR